递归 Recursion#

By Danny_Chen

引言#

大家好！相信不管是CSC1001还是CSC1003的同学都已经学习了递归(Recursion)这个概念，它似乎比较抽象，但却是计算机思维中非常重要的一部分。虽然在工程中因复杂度太高，基本都会将递归改为非递归(除非确定数据量再大递归也不深)，但这种递归的思维会陪伴我们的整个计算机学习过程和对计算机的理解过程，在计算机和编程的学习中至关重要。

这篇文章中，我们将讨论递归算法的思想，底层原理，优化和应用。

什么是递归？#

首先，让我们从定义入手。

递归的定义是？请参见“递归”。

啊？这个定义不是相当于什么都没说吗？但这就是“递归”的含义。什么含义呢？即自己调用自己。

大家可能会发现，在数学中的许多定义都属于“递归定义”(recursive definition)。让我们通过这些定义理解：

• 正整数

正整数是怎么定义的？肯定不是$n = 1, 2, 3, ......$，这样太不严谨了。正确的定义应该是：

1. $1$是正整数
2. 如果$n$是正整数，$n+1$也是正整数
3. 正整数集是满足$(1)(2)$的最小集

我们发现，在这个定义中就使用了递归的思想，即在“正整数”还未完全定义时，就用到了“正整数”的定义。

举个例子，$3$是不是正整数？我们把$3$看做$n+1$，那么$n$就是$2$，$2$是不是正整数？我们再把$2$看做$n+1$，那么$n$就是$1$，$1$是不是正整数？这里，通过定义中的$(1)$，是的！那么我们就可以推断出来，3是正整数！

这就是递归的定义。即从结果入手，不断递推向前，直到找到一个明确定义，返回最终结果。

如果是SDS的同学，我们在Lec18中已经学习了行列式Determinant的定义，这也是一个典型的递归定义。

• 行列式

上课时所讲的行列式的定义是这样的：

For a scalar $α ∈ R$, define $det(α) = α$.

For any $A ∈ R^{n×n}$ with $n ≥ 2$ define

在行列式的定义中，我们不断地把$n×n$的矩阵A缩小，直到缩小到2×2时，我们终于可以计算其行列式等于$ad-bc$，如此，我们就可以递归计算任何$n×n$矩阵的行列式了！

所以我们可以看到，递归的初步思想其实就是把大问题逐步缩小，直到变成最小的同类问题的过程，而最后的小问题的解是已知的。

好了，递归的定义就到这里，下面我们来看一下递归函数。

递归函数#

在编程语言中实现递归，我们就要用到递归函数，什么是递归函数呢？递归函数怎么写呢？我们来看一个例子。

求阶乘#

这个问题应该是递归最简单的应用了。阶乘函数$f(n) = n!$可以被定义为：

使用编程实现求一个数的阶乘，我们便可以使用递归的方法解决。下面我们来看一下相应的代码(这里只写出递归函数)。

C++:

int factorial(int n){
    if(n == 0) return 1;//base case
    else return factorial(n - 1) * n;//reduction step
    //return n == 0 ? 1 : factorial(n - 1) * n;//简化写法：三元运算符
}

Java:

public static int factorial(int n){
    if(n == 0) return 1;//base case
    else return factorial(n - 1) * n;//reduction step
    //return n == 0 ? 1 : factorial(n - 1) * n;//简化写法：三元运算符
}

Python:

def factorial(n):
    if n == 0: 
        return 1  ##base case
	else: 
        return factorial(n - 1) * n  ##reduction step

大家可以发现，我将这段代码注释成了两部分：base case和reduction step，分别指边界条件和递归方程，也就是递归函数的两个基本组成部分。什么是边界条件？即我们最终化成的已知解的小问题(例如第一部分中我们提到的，$1$为正整数，$2×2$的行列式可解，还有本题中的$0$的阶乘是$1$)。什么是递归方程？即我们把一个大问题逐步缩小的过程，我们可以把它类比为数列的通项公式，即从$a(n)$回溯到$a(1)$的过程。

更直观一点，我们来模拟一下这个函数的运行过程：

假设$n = 3$，我们来进行模拟。

向上递归过程：

$n = 3 → n ≠ 0 → else →$执行$f(2) * 3$

$n = 2 → n ≠ 0 → else →$执行$f(1) * 2$

$n = 1 → n ≠ 0 → else →$执行$f(0) * 1$

$n = 0 → n == 0 →$返回$1$

向下递归过程：

$n = 0 → n == 0 →$返回$1$

$n = 1 →$执行$f(1)$ $=$ $f(0)$ $*$ $1$ $=$ $1$ $*$ $1$ $=$ $1$

$n = 2 →$执行$f(2)$ $=$ $f(1)$ $*$ $2$ $=$ $1$ $*$ $2$ $=$ $2$

$n = 3 →$执行$f(3)$ $=$ $f(2)$ $*$ $3$ $=$ $2$ $*$ $3$ $=$ $6$

最终返回值：$6$

递归的底层原理#

通过上面这个例子，我们能够很清晰的看到递归的运算过程，大家可以发现，我将递归的运算过程分为了“向上递归过程”、“向下递归过程”和“最终返回值”。为什么要这么去分呢？原因在于，递归的实现借助了计算机的系统栈。

什么是栈(stack)？#

栈是一种数据结构，符合LIFO(后进先出)的规则。我们借助图示来理解。

正如大家所见，现在这里有一个开口的长方形箱子，它存在于内存中，我们将它称之为栈。

我们可以在里面放东西，比如……

我现在放进去了一个小盒子，把它取名叫"$3$"，它现在出现在大箱子“栈”的最底部(栈底)。如此，我们继续往里放小盒子"$2$''，"$1$"，"$0$"。

好的，现在大箱子被堆满了！以上这个堆箱子的过程，我们称为“入栈”。在上面我对递归的描述中，对应“向上递归过程”，即从$f(3)$一直回溯到$f(0)$的过程。

现在，我们要开始把小盒子都拿出来了。

毫无疑问，我们只能先将"$0$"从大箱子中拿出来，这就是所谓的LIFO(后进先出)，我们一步步的将小盒子从栈顶拿出，直到将栈清空，这个过程叫“出栈”。在上面我对递归的描述中，对应“向下递归过程”，即从$f(0)$一直返回到$f(3)$的过程。

最终经过一步步返回，小盒子"$3$"中储存的值，就是“最终返回值”。

系统栈与递归#

这里要注意，系统在运行递归的时候，会开辟一个空间叫“系统栈”，而系统在帮你压栈。我们来仔细分析一下过程，还是以上面阶乘为例：

1. 首先，系统把初始值$n = 3$放入栈底，进行运算。显然，在运算过程中，出现了未知的值$f(2)$，这时，系统就会保留栈底，转而运行子过程$n = 2$，将子过程压于栈底上方;
2. 同样的，在运算$n = 2$时，出现了未知的值$f(1)$，系统保留这个过程后，去运算子过程$n = 1$，将其继续压于上方……；
3. 当运算到过程$n = 0$时，终于能够找到明确的返回值，就从栈顶$n = 0$开始出栈，一步一步将值返回到栈底，填补前面过程的未知值，直到最终计算出$n = 3$时的返回值退出函数。

但是，系统栈的空间是独立的，比较”贵“，容量比较小，若这个空间满了，就会报错，在工程中并不安全。

所以我们可以提出一种优化方法，即“手写栈”，我们可以在内存中申请一个栈空间，模拟系统栈的运行方式。内存空间会比较“便宜”，给到我们的容量很大，从而使得程序更加安全。

好了，以上就是递归的底层原理，即通过“系统栈”的入栈出栈来实现递归过程。

递归的优化#

现在我们再来看一个经典的问题。

斐波那契数列：给出$n$，输出斐波那契数列的第$n$项。#

这个问题最简单的实现方式就是通过递归，我们来看一下代码，这里还是只给出递归函数。

C++:

int Fibonacci(int n){
    if(n == 1) return 1;
    if(n == 2) return 2;
    else return Fibonacci(n - 1) + Fibonacci(n - 2);
}

Java:

public static int Fibonacci(int n) {
	if (n == 1) return 1;
    if (n == 2) return 1;
    else return Fibonacci(n - 1) + Fibonacci(n - 2);
}

Python:

def Fibonacci(n):
    if(n == 1): 
        return 1
	if(n == 2): 
        return 1
	else: 
        return Fibonacci(n - 1) + Fibonacci(n - 2)	

以上就是斐波那契数列求值的递归实现方法。

但是，如果我们令输入的$n = 50$，却迟迟没有得到结果，只得到了风扇的轰鸣声……

这是为什么呢？

我们使用树状图表示一下这个递归过程。(这里借用一下老师上课的图)

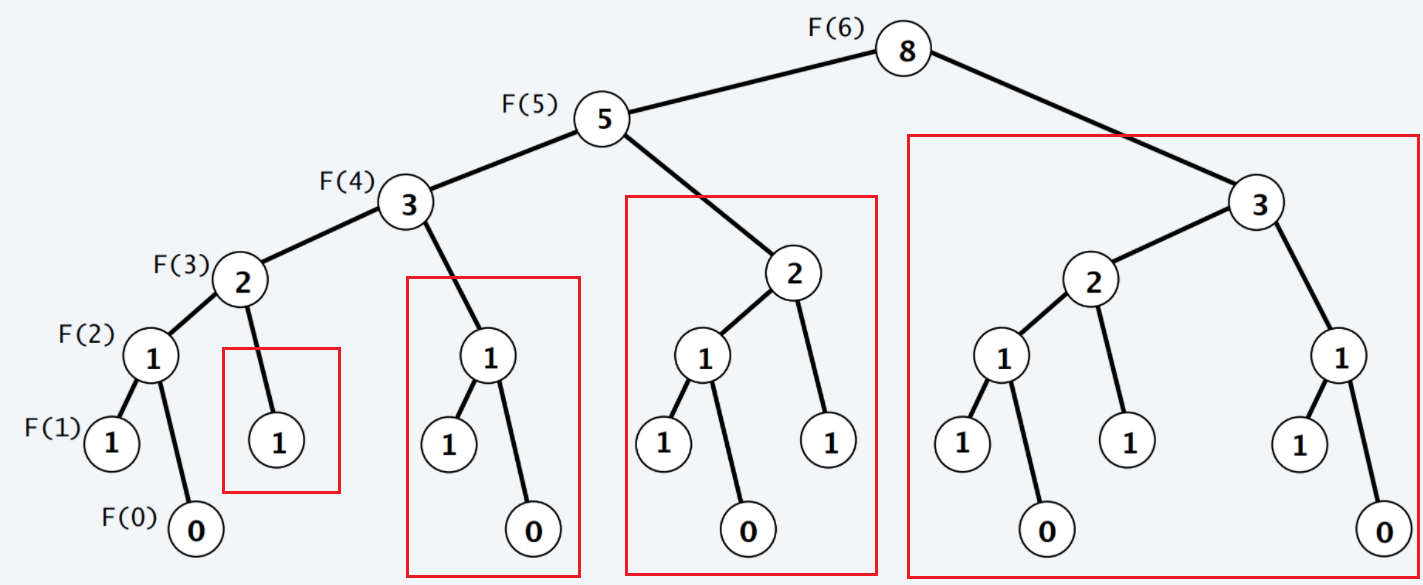
注意一下我用红色方框标注出来的部分，我们可以发现许多项都被重复计算了很多次，造成了复杂度的极度浪费。使得这个程序使用$O(2^{n})$的复杂度完成$O(n)$的任务，导致计算机无法计算。

那么想必大家已经发现了解决措施，如果我们把每一项都只计算一次，将这个结果单独储存起来，是不是就能解决这个问题呢？

下面，我们来看一下代码。

C++:

long long arr[1000] = {};
long long Fibonacci(int n){
    if(n == 1) return 1;
    if(n == 2) return 1;
    if(arr[n] == 0) arr[n] = Fibonacci(n - 1) + Fibonacci(n - 2);
    return arr[n];
}

Java:

static long[] arr = new long[1000];
public static long Fibonacci(int n) {
    if (n == 1) return 1;
    if (n == 2) return 1;
    if(arr[n] == 0) arr[n] = Fibonacci(n - 1) + Fibonacci(n - 2);
    return arr[n];
}

Python:

arr = [0] * 1000
def F(n):
    if n == 1:
        return 1
    if n == 2:
        return 1
    if arr[n] == 0:
        arr[n] = F(n - 1) + F(n - 2)
    return arr[n]

现在，程序的时间复杂度回到$O(n)$，我们可以计算更大项数的斐波那契值了！

下面是题外话：为方便笔者复习使用，这里贴出大数斐波那契的写法(结合高精度算法)，使用Java实现。

public class LargeFib {
  public static void main(String[] args) {
    int n = Integer.parseInt(args[0]);
    int d = 10000;

    int[] a = new int[d];
    int[] b = new int[d];
    a[0] = 1;  //fib(0)
    b[0] = 1;  //fib(1)
    int i;

    //calculate fib(n) (n >= 2)
    for (i = 2; i < n; i ++ ) {
      //a = a + b; c = b; b = a; a = c;
      int carry = 0;
      for(int j = 0; j < d; j ++ ){
        a[j] = a[j] + b[j] + carry;
        if(a[j] < 10) carry = 0;
        else{
          carry = 1;
          a[j] = a[j] - 10;
        }
      }
      int[] c = b;
      b = a;       //fib(i) = b now!
      a = c;
    }
    //output the result
    for(i = n - 1; b[i] == 0; i -- );  //find the first nonzero element in b
    for(int j = i; j >= 0; j -- ){
      System.out.print(b[j]);
    }
    System.out.println();
  }
}

递归的应用#

在这个板块，我们只来分析一个问题，即汉诺塔问题。

汉诺塔问题(Hanoi Tower Puzzle)#

汉诺塔由三根柱子（分别用L、M、R表示）和n个大小互不相同的空心盘子组成。一开始$n$个盘子都摞在柱子M上，大的在下面，小的在上面，形成了一个塔状的锥形体。 对汉诺塔的一次合法的操作是指：从一根柱子的最上层拿一个盘子放到另一根柱子的最上层，同时要保证被移动的盘子一定放在比它更大的盘子上面（如果移动到空柱子上就不需要满足这个要求）。汉诺塔的游戏目标是将所有的盘子从柱子M移动到柱子R上面。

这是一个经典且难度较大的问题，我们尝试去解决它。

首先我们从最简单的情况开始，通过画图的方式直观理解这个问题。

• $n = 1$ (base case):

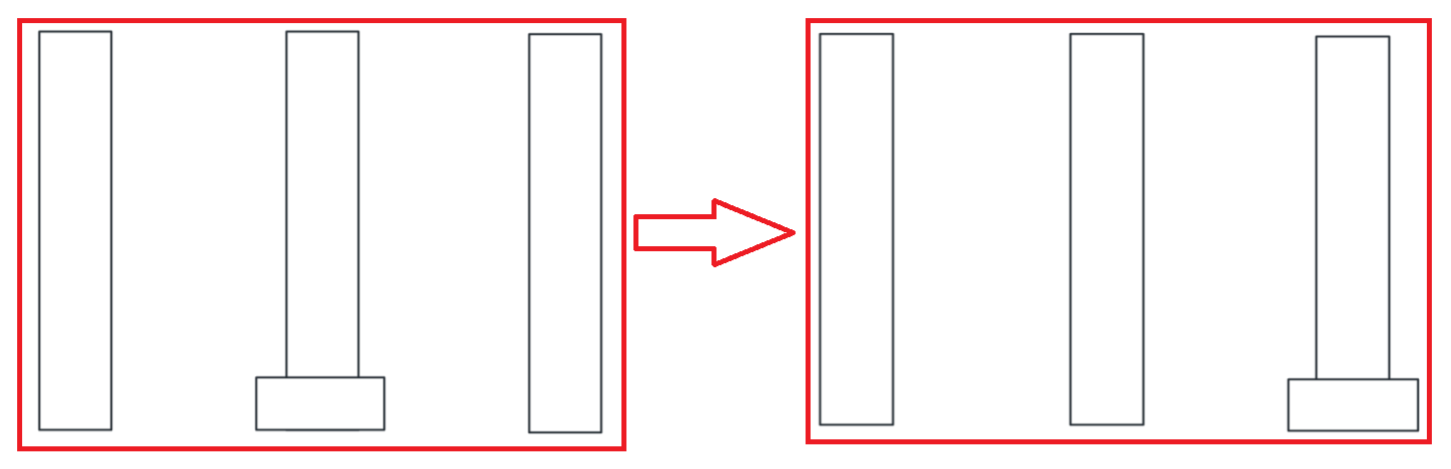
嗯……这个应该不用讲了。直接把盘子从M柱移到R柱即可。步骤：

将$1$个盘子从M移到R ( 图2 )

• $n = 2$ :

这个情况也不难，三步就可以解决。首先，我们把小盘子从M柱挪到L柱，在这里，L柱并不是最终的目标柱，我们可以把它想象为临时的“休息站”，先把小盘子停在这休息。然后，我们就可以把大盘子从M柱挪到目标柱R柱，再把停在“休息站”L柱的小盘子挪到R柱，即可完成。

简单来说，我们可以将步骤概括为：

1. 将$1$个盘子从M移到L ( 图2 )
2. 将第$2$个盘子从M移到R ( 图3 )
3. 将$1$个盘子从L移到R ( 图4 )

• $n = 3$ :

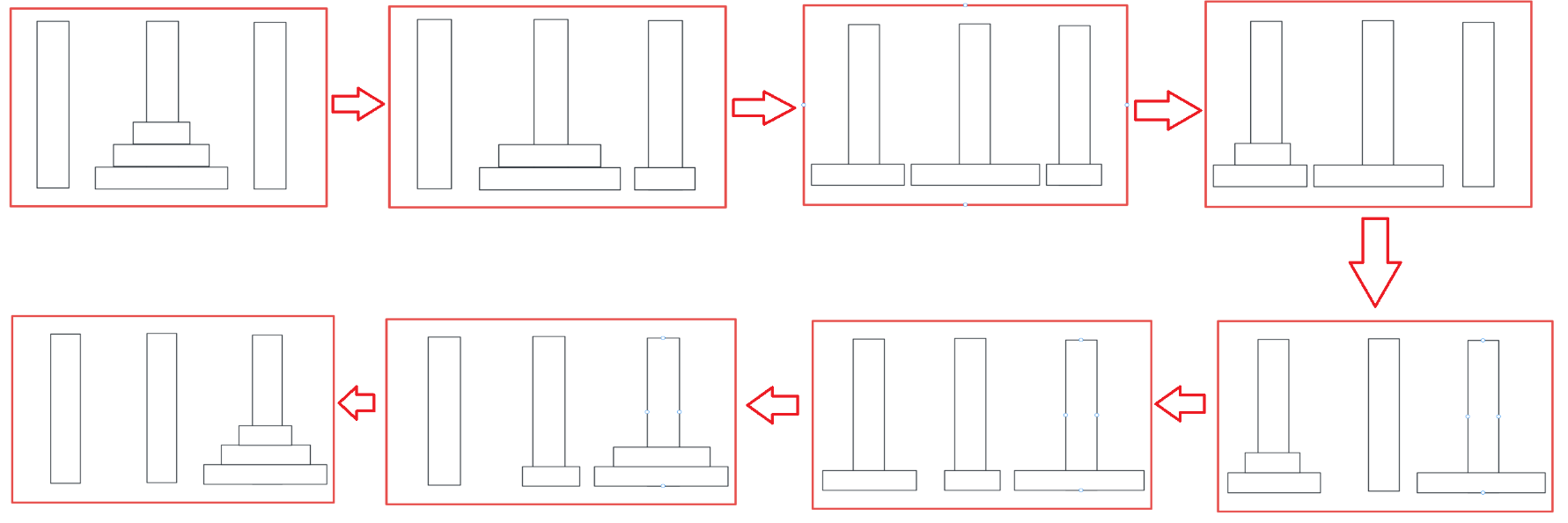
我们一共需要7步解决$n=3$的汉诺塔问题。依然是通过“起始站”、“终点站”、“休息站”来进行。

简单来说，我们可以将步骤概括为：

1. 将$2$个盘子从M移到L ( 图2 ~ 4 )
2. 将第$3$个盘子从M移到R ( 图5 )
3. 将$2$个盘子从L移到R ( 图6 ~ 8 )

• $......$

• 所以现在我们可以总结出解决汉诺塔问题的步骤，即$n$层汉诺塔：

1. 将$n-1$个盘子从M移到L
2. 将第$n$个盘子从M移到R
3. 将$n-1$个盘子从L移到R

不难发现，这里面隐含着递归的思想：

解决$n$层的汉诺塔问题

$→$ 解决$n-1$层的汉诺塔问题

$→$ $......$

$→$ 解决$1$层的汉诺塔问题

那么，到解决一层的汉诺塔问题，就变得非常简单了！

下面，我们写出汉诺塔问题的代码，这次给出全部代码。我将注释写在Java代码后面，大家可以对照前面的分析来看代码。

C++:

#include <iostream>
using namespace std;

void move(int n, string from, string to, string help) {
    if (n == 1) {
        cout << from + " ==> " + to << endl;
        return;
    }//n = 1时的base case,直接可以从起始站移到终点站
    move(n-1, from, help, to);//将n-1个盘子从起始站移到休息站
    cout << from + " ==> " + to << endl;//将第n个盘子从起始站移到终点站
    move(n-1, help, to, from);//将n-1个盘子从休息站移到终点站
}

int main() {
    int N;
    cin >> n;
    move(N, "MIDDLE", "RIGHT", "LEFT");
    return 0;
}

Java:

public class Main {
  public static void main(String[] args) {
    int N = Integer.parseInt(args[0]);
    move (N, "MIDDLE", "RIGHT", "LEFT");
  }

  public static void move(int n, String from, String to, String help){
    if (n == 1){
      System.out.println(from + " ==> " + to);
      return;
    }//n = 1时的base case,直接可以从起始站移到终点站
    //n > 1
    move(n-1, from, help, to);//将n-1个盘子从起始站移到休息站
    System.out.println(from + " ==> " + to);//将第n个盘子从起始站移到终点站
    move(n-1, help, to, from);//将n-1个盘子从休息站移到终点站
  }
}

Python:

def move(n, from_rod, to_rod, aux_rod):
    if n == 1:
        print(from_rod + " ==> " + to_rod)
        return ##n = 1时的base case,直接可以从起始站移到终点站
    move(n-1, from_rod, aux_rod, to_rod) ##将n-1个盘子从起始站移到休息站
    print(from_rod + " ==> " + to_rod) ##将第n个盘子从起始站移到终点站
    move(n-1, aux_rod, to_rod, from_rod) ##将n-1个盘子从休息站移到终点站

N = int(input())
move(N, "MIDDLE", "RIGHT", "LEFT")

结语#

如果你看到了现在，恭喜你已经掌握了递归这个编程中最基本最重要的思想之一！之后我们将学习的一些算法也都是基于递归思想去实现的，希望大家都能在以后的学习中游刃有余。

感谢观看！